XXXI. Группа движений
Однако в отношении всех этих интерпретаций остается вопрос, который здесь еще не выяснен. Как понимать в этих своеобразных интерпретациях движение? Чтобы это себе уяснить, нужно прежде всего обратить внимание на следующее. В геометрии мы постоянно пользуемся движением; оно играет очень важную роль в наших рассуждениях и доказательствах; а между тем фактически мы его никогда не производим. Когда мы говорим: наложим треугольник ABC на треугольник А'В'С', то мы ведь в действительности не переносим треугольника на другое место,— это и невозможно. Если вникнем в то, чем мы собственно интересуемся, когда пользуемся в геометрии движением тела, то увидим, что нам всегда важно только знать, с какой точкой при этом совмещается каждая точка переносимого тела.
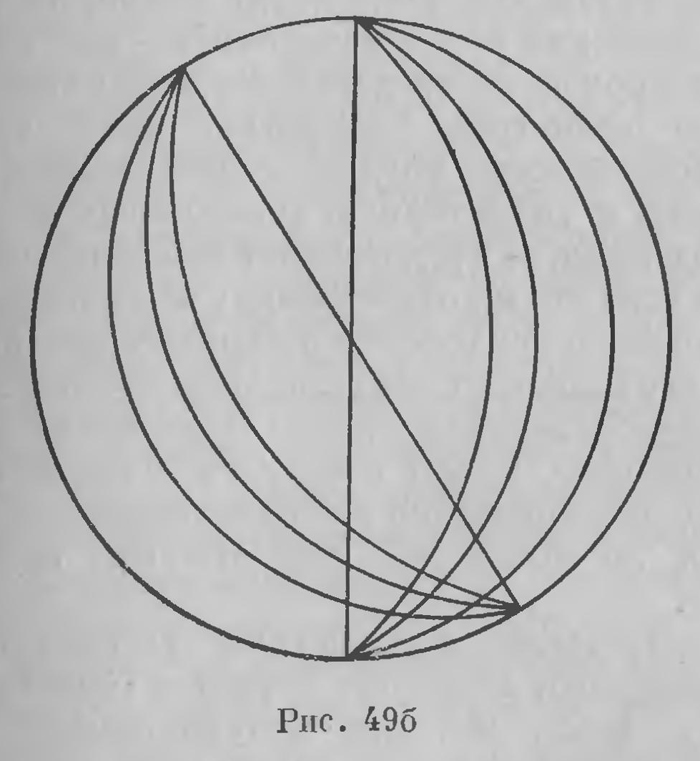
Каждой точке А первого тела отвечает некоторая точка А' второго тела, с которой она совмещается после перенесения. Мы устанавливаем, таким образом, соответствие между точками первого и второго тела; мы мысленно осуществляем это соответствие при помощи движения, так как точка А' второго тела есть та, в которую движение переносит точку А. Но если мы то же соответствие установим как-нибудь иначе, то роль механического движения будет исчерпана,— оно уже не будет нужно. Этот процесс не представляет исключительной принадлежности геометрии; напротив, это — чрезвычайно важное, неотъемлемое орудие нашей мысли. «Чрезвычайно важную и характерную способность нашего ума — говорит Дедекинд,— представляет собой процесс, заключающийся в том, что мы относим одну вещь к другой». Этот процесс в логике и психологии называют ассоциацией; в математике его называют сопряжением одного множества с другим, отображением одного множества на другом. Второе множество может совпадать с первым; мы тогда говрим, что оно приведено в соответствие с самим собой, отображено на самом себе или что оно преобразовано в самое себя. Такое соответствие в геометрии устанавливают движением; более того, движение играет в геометрии исключительно ту роль, что оно устанавливает некоторое отображение пространства на самом себе. Чтобы это лучше выяснить, возьмем простой пример. Пусть АВ будет некоторый отрезок. Каждой точке С этого отрезка, которая отстоит на расстояние с от точки А, мы примем в качестве соответствующей точку С', отстоящую на то же расстояние с от точки В. Этим каждой точке отрезка будет отнесена другая точка, отрезок будет отображен на самом себе. Это отображение, это соответствие, может быть также осуществлено движением, если мы новернем отрезок, наложим его на себя другой стороной; каждая точка С упадет при таком движении в соответствующую точку С'. Заметим при этом следующее. Положим, что некоторое движение совмещает тело А с телом В. Мы всегда можем представить себе неизменяемую среду, неразрывно связанную с телом А и охватывающую все пространство. Движение совмещает каждую точку этой среды с некоторой точкой пространства; мы можем, таким образом, сказать, что движение устанавливает соответствие всего пространства, множества, которое это пространство представляет, с самим собой, отображает его на самом себе. В этом смысле мы всегда будем говорить не о движении тела в пространстве, а о движении всего пространства в самом себе, об отображении всего множества на самом себе. Итак, геометрическое движение, т. е. движение, как мы им пользуемся в геометрии, всегда можно рассматривать как отображение всего пространства, всего множества, в котором мы оперируем, па самом себе. Однако в пространстве существует не одно, а бесчисленное множество движений. Это значит, что каждое тело в пространстве допускает многообразные перемещения, а вместе с тем осуществляются многообразные движения самого пространства, многообразные отображения его на самом себе. Вся эта совокупность отображений обладает некоторыми существенными особенностями. Не останавливаясь на простейших из них, связанных с некоторым уточнением самого понятия об отображении (его однозначность и непрерывность), мы укажем только на две важнейшие их особенности. Первая заключается в том, что если некоторое движение совмещает тело А с телом В, так что каждая точка М тела А приходит в совмещение с точкой М' тела В, то существует и «обратное» движение, которое совмещает тело В с телом А и притом так, что каждая точка М' тела В «обратно» совмещается с соответствующей точкой М тела А. Вторая особенность состоит в следующем: положим, что некоторое движение совмещает тело А с телом В, а затем другое движение совмещает тело В с телом С; в таком случае всегда существует третье движение, которое непосредственно совмещает тело А с телом С. Иными словами, совокупность тех отображений, которые геометрически осуществляют совокупность движений в пространстве, обладает тем свойством, что каждым двум отображениям этой совокупности всегда отвечает третье, заменяющее последовательное выполнение их. Эти два свойства системы отображений очень часто встречаются в математике и помимо движений. Если совокупность отображений или преобразований обладает теми свойствами, что каждому ее преобразованию отвечает в той же совокупности обратное преобразование и двум последовательным ее преобразованиям в той же совокупности всегда отвечает третье преобразование, заменяющее последовательное производство их, то говорят, что такая совокупность отображений образует группу. В соответствии с этой терминологией можно сказать, что совокупность движений пространства с геометрической точки зрения составляет группу отображений.. Имея в виду метрическую геометрию, отметим еще одну важную особенность этих отображений. Расстояние между двумя точками при установленной единице меры выражается некоторым арифметическим числом. Если какое-либо движение приводит точки А и В в совмещение с точками А' и что расстояние АВ должно быть равно расстоянию А'В'. С точки зрения учения о группах это выражается следующим образом. Каждым двум точкам пространства отвечает число, остающееся неизменным при всех отображениях группы,— инвариант этой группы. Если возьмем некоторую совокупность точек, то для каждых двух из них этот инвариант — расстояние — имеет определенное значение; инвариантной остается и каждая комбинация парных инвариантов, каждая функция от них. Но для данной совокупности точек не существует инварианта, который от парных инвариантов не зависит. Чтобы это выяснить, остановимся на совокупности трех точек; они определяют треугольник, он имеет определенную площадь; это тоже есть инвариант движения. Но хорошо известно, что площадь треугольника выражается через длины его сторон, т. е. через парные инварианты. Группа движений пространства допускает инвариант двух точек, но не имеет независимого инварианта большего числа точек. Вместе с тем геометрия, построенная на движении, имеет своим содержанием изучение той группы отображений множества, которая составляет основу его геометрии. Эта точка зрения с полной определенностью, с существенным обобщением, о котором мы сейчас скажем, была впервые высказана Феликсом Клейном. В 1872 г. Клейн, вступая на кафедру математики в Эрлангенском политехникуме, произнес программную речь, темой которой служили новые взгляды на сущность геометрии. Эта речь, известная под названием «Эрлангенской программы», сыграла чрезвычайно важную роль в деле установления взглядов на сущность геометрии, в частности — в выяснении того места, которое занимает геометрия Лобачевского1. Сущность взглядов Клейна заключается в следующем. Чтобы построить геометрию, нужно прежде всего установить то множество, в котором мы геометрию строим, которое служит ее субстратом. Затем нужно установить ту группу отображений этого множества в самом себе, которая собственно геометрию определяет, т. е. отличает ее от всякой другой геометрии, которая может быть построена в этом же множестве. Основное содержание геометрии составляет изучение инвариантов этой группы отображений. Остановимся теперь на метрической геометрии, допускающей такие движения, что в ней каждая точка может быть совмещена с каждой другой точкой; говорят, что группа движений в такой геометрии транзитивна. Но вместе с тем группа такой геометрии, как мы видели, Должна состоять из отображений, по отношению к которым всякие две точки имеют инвариант, а большее число точек независимого инварианта не имеет. Известный норвежский математик Софус Ли, детально разработавший учение о группах непрерывных отображений, показал, что существуют только три группы, удовлетворяющие этим требованиям, а эти три группы приводят к трем геометрическим системам — Евклида, Лобачевского и Римана. Таким образом, возможны только три системы метрической геометрии, основанные на движении. Простейшая из них — старая геометрия Евклида. Лобачевский открыл вторую метрическую геометрию — гиперболическую. Третья — эллиптическая, в двумерной области, на сфере, также была известна еще в древности; Риман показал, что она может существовать и в трехмерном пространстве. Клейном и Ли установлена точка зрения на геометрию, которая, с одной стороны, выясняет, где коренился источник ее расширения, а с другой — устанавливает и пределы расширения, допускаемые метрической геометрией. Однако точка зрения Клейна и Ли допускает не только метрическую геометрию. Возможны геометрические системы, оперирующие такими группами, в которых две точки не имеют инварианта; в такой геометрии двум точкам не соответствует расстояние, в нем невозможно измерение, это не метрическая геометрия. Такова группа, на которой строится так называемая проективная геометрия. Проективная геометрия получила в настоящем столетии очень широкое развитие; построена даже дифференциальная проективная геометрия широкого охвата2. На группе так называемых аффинных преобразований строится аффинная геометрия, элементарная и дифференциальная; на группе конформных преобразований строится конформная геометрия, также получившая дифференциальное развитие. Остановимся еще на проективной геометрии, к которой нас возвратит интерпретация неевклидовой геометрии на основном круге. В проективной геометрии численный инвариант имеют только четыре точки, и притом расположенные на одной прямой,— это их ангармоническое отношение. Основная характеристика проективных отображений заключается в том, что они всегда отображают прямую прямой же; и обратно, всякое отображение, которое представляет собой коллинеацию, т. е. в котором отображением прямой всегда служит прямая, есть проективное отображение. Это дает ключ к выяснению метрики в интерпретации геометрии Лобачевского на бельтрамиевом круге. Каковы те отображения на основном круге, которые в установленном выше смысле соответствуют движениям гиперболической плоскости? Эти движения, конечно, переводят прямые в прямые; соответствующие отображения на основном круге переводят одни его хорды в другие, т. е. опять-таки переводят прямые в прямые же; это должны быть, следовательно, проективные преобразования. С другой стороны, бесконечно удаленные точки гиперболической плоскости при движении никогда не могут перейти в конечные (это собственно означает, что параллельные линии всегда переходят в параллельные же). Соответственно этому на такой карте при каждом отображении, соответствующем гиперболическому движению, граничный круг переходит сам в себя. Таким образом, отображения, которые на основном круге соответствуют гиперболическим движениям, суть проективные преобразования, которые преобразуют окружность этого круга в себя самое. Эта группа отображений, эта подгруппа всех проективных преобразований плоскости допускает очень простое, очень изящное аналитическое выражение; ее установлением завершается отображение двумерной гиперболической (плоскости на евклидовом круге; аналогично проводится отображение гиперболического пространства на шаре. Одно обстоятельство способно, однако, вызвать здесь недоумение. Ведь при проективном преобразовании инвариант имеют только четыре коллинеарные точки, а не две; каким же образом здесь, на нашей карте, выплывает расстояние между двумя точками? Это объясняется очень просто. Дело в том, что здесь, на основном круге, любые две точки А и В определяют две другие точки, именно точки Р и Q (рис. 50) пересечения прямой с окружностью круга. Этот комплекс четырех точек (АВ, PQ), а вместе с тем их ангармоническое отношение вполне определяются двумя точками А и В - это ангармоническое отношение представляет собой инвариант рассматриваемых отображений, оно определяет расстояние между точками А и В. Нужно только это ангармоническое отношение надлежащим образом выбрать; необходимо так его нормировать, чтобы было соблюдено свойство аддитивности, которое здесь нужно понимать следующим образом. 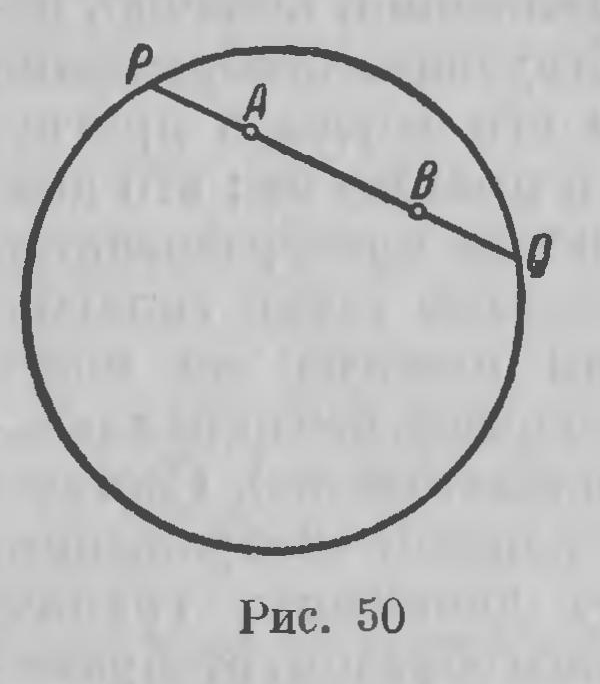
Если С есть точка, лежащая на прямой АВ между точками А и В, то расстояние АВ должно равняться сумме расстояний AC + СВ. Заметим, что этому требованию удовлетворяет следующая функция от ангармонического отношения: 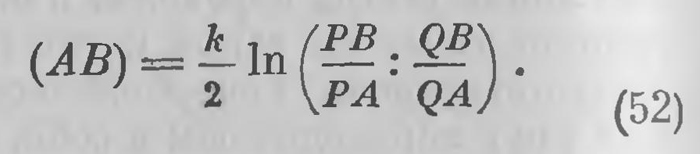
И именно ее значение принимается за расстояние между точками А и В в этой модели гиперболической плоскости. Читателю может показаться странным такое своеобразное, на первый взгляд сложное, выражение, принимаемое за расстояние между двумя точками. Но внимательно в него всмотревшись, нетрудно себе уяснить, что к нему привело. Прежде всего ясно, что при этом выборе ангармонического отношения число РВ/РА всегда больше единицы, а число QB/QA меньше единицы. Под знаком логарифма всегда стоит положительное число, большее единицы, а поэтому выражение для расстояния всегда имеет положительное значение. Оно обращается в нуль только в том случае, если эти две дроби равны, а это возможно только тогда, когда точка А совпадает с точкой В; в этом — и только в этом — случае расстояние (АВ) обращается в нуль. Легко также видеть, что это выражение неограниченно возрастает, когда точка А стремится к Р или точка В стремится к Q; точки окружности суть бесконечно удане точки плоскости. Наконец, если точка С лежит между А и В, то по той же формуле (52) 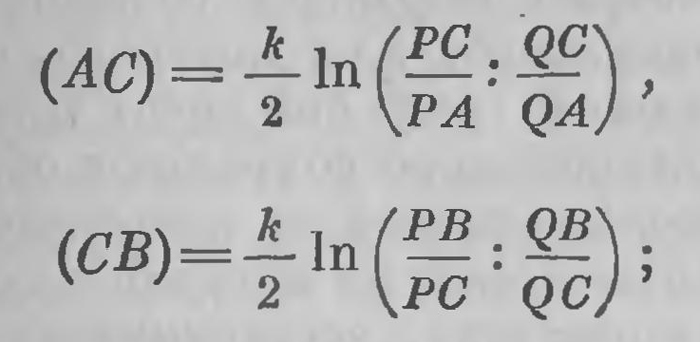
и совершенно ясно, что (АВ)=(АС)+(СВ), так называемое требование аддитивности выполняется. Отображение гиперболической плоскости на евклидовом (бельтрамиевом) круге выполнено совершенно безукоризненно; двумерная гиперболическая геометрия осуществляется здесь полностью. Совершенно аналогично выполняется отображение гиперболического пространства внутри евклидовой сферы. Всякое противоречие в гиперболической геометрии, если бы оно обнаружилось, означало бы, что аналогичное противоречие имеется и в геометрии Евклида. Поэтому гиперболическая геометрия логически столь же правильна, столь же непротиворечива, как и геометрия Евклида. Таким образом, к тому времени, как исполнилось сто лет со дня рождения Лобачевского, сомнений в логической правильности, в непротиворечивости созданной им геометрии, можно сказать, уже не было. Задача, которая стояла перед Лобачевским всю его жизнь, была окончательно разрешена. Исследования же, которые привели к этому решению, выдвинули ряд глубоких идей, установили совершенно новый взгляд на геометрию, определили широкую ее эволюцию. Первая, может быть, важнейшая из этих идей заключалась в том, что геометрия свойственна не только пространству в том смысле, как его всегда понимали. Совершенно так же, как для выражения соотношений между пространственными образами была построена классическая геометрия, можно строить геометрию, — вернее, геометрии,— для различных многообразий (множеств); каждая такая геометрия выражает соотношения, имеющие место в том множестве, для которого она построена. Общее название «геометрии» они носят потому, что в своем строении в некоторой мере сохраняют общую схему, общий облик, унаследованный от классической геометрии; но по существу эти геометрии могут быть очень различны, как различны множества, составляющие их субстрат, и соотношения, которые в них имеют место. Вторая, тесно с этим связанная идея, заключается в том, что одна и та же геометрия может получать применение, может осуществляться не только в одном, но и в различных множествах; эти множества называются различными интерпретациями этой геометрии или различными ее моделями. Существование конкретной интерпретации, в которой геометрическая система выполнена, устанавливает ее непротиворечивость. Попытки применять геометрию не к тому множеству, к которому она приспособлена, в котором она осуществляется, а к другому, существенно от него отличному, естественно приведет к нелепости. Именно этого рода видимая нелепость стояла на пути усвоения геометрии Лобачевского. Геометрия может быть, таким образом, многообразна. Построение геометрии требует прежде всего установления множества, которое служит ее субстратом. Дальнейший путь может быть двояким. Можно установить группу отображений или преобразований этого множества, которой определяется его геометрия; это установка Клейна и Ли. Можно определить мероопределение множества метрической квадратичной формой — это точка зрения Римана. В весьма замечательной работе Гельмгольца можно усмотреть связь, которая эти точки зрения объединяет3. По этим путям быстрыми шагами пошла эволюция геометрии. Эта эволюция заключалась в установлении новых разновидностей уже известных геометрических систем, f18расширении содержания каждой геометрии, разыскании новых интерпретаций (моделей) этих геометрий, развитии геометрий различных групп преобразований, построении общей теории римановой геометрии. Но и на этих замыслах эволюция геометрии отнюдь не остановилась. Мы не имеем возможности описать здесь дальнейшие пути, по которым она шла; отсылая читателя к специальным сочинениям, сюда относящимся4, мы только еще раз подчеркнем, что все это обилие идей и фактов имело своим источником творения Лобачевского. Они имели и другие далеко идущие результаты, которым посвящена заключительная глава. К столетию со дня рождения Лобачевского его имя было у всех на устах, пользовалось признанием и самой почетной известностью. В 1893 г. Казанским университетом и Казанским физико-математическим обществом было организовано празднование столетнего юбилея со дня рождения Лобачевского. На это торжество откликнулись ученые и научные учреждения всего мира5. Затем (в 1895г.) Казанским физико-математическим обществом была учреждена премия Н. И. Лобачевского для увековечения его имени. Капитал для этого (6000 руб. золотом) был собран по подписке, в которой участвовали ученые всего мира. Присуждение премии (по 500 руб. каждая) должно было происходить через каждые три года; но после пятого конкурса первая мировая война нарушила эти сроки. На премию представили свои работы самые выдающиеся геометры мира. Первым лауреатом (1896 г.) был Софус Ли. Последний (довоенный) конкурс состоялся в 1937 г. На этот раз Общество располагало тремя премиями: международной премией в 1000 руб. и двумя премиями для советских молодых ученых по 500 руб каждая. Согласно распоряжению Народного комиссариата просвещения Общество предложило молодым ученым для получения премии две темы, связанные с развитием неевклидовой геометрии. Международная премия была присуждена члену Парижской Академии наук Эли Картану, а обе советские премии получил профессор Саратовского университета В. В. Вагнер6. Отзывы о представленных сочинениях по поручению Казанского физико-математического общества составлялись выдающимися представителями математических наук. Так, отзыв о работах Софуса Ли был дан Ф. Клейном7. Эти отзывы содержали обыкновенно и собственные рассуждения авторов о вопросах обоснования математики. Казанское общество опубликовало протоколы присуждения премий в своих «Известиях»; они выпущены также отдельными изданиями. Собрание этих протоколов содержит очень ценный материал по вопросам логического обоснования математики. В настоящее время по ходатайству президиума Академии Наук СССР международная премия имени Н. И. Лобачевского вновь восстановлена. Она будет выдаваться за выдающиеся работы по геометрии, преимущественно неевклидовой. Присуждение премии будет производиться в Казани выездной сессией Академии Наук СССР. Первое присуждение будет происходить в 1950 г. В 1893 г. во время празднования столетнего юбилея со дня рождения Лобачевского в Казанском физико-математическом обществе возникла мысль о постановке ему памятника. Этот замысел был осуществлен. Памятник был поставлен в сквере, специально для этого устроенном перед зданием университета. Он был открыт 1 (13) сентября 1896 г. 1F. Klein. Vergleichende Betrachtungen iiber neuere geometrische Forschungen. Erlangen, 1872. Русский перевод помещен в Известиях Казанского физ.-мат. общества» за 1896 г. Оттиски выпущены отдельным изданием. 2См. С. Фиников. Проективная дифференциальная геометрия. М. — Л., 1937. 3Н. Helmholtz. Ueber die Thutsachen, die der Geometrie zu Grunde liegen. Gottingen. Gel. Nacliricliten, 14, 1888. 4I. A. Schouten und D. Dаntzig. Was ist Geometrie? Труды Семинара по векторному и тензорному анализу, II—III. 5«Празднование Казанским университетом столетней годовщины со дня рождения Н. И. Лобачевского». Казань, 1894. 6Отчеты по присуждению премий публиковались в «Известиях Казанского физико-математического общества» и выпускались отдельными изданиями в 1898, 1901, 1904, 1907, 1910, 1914, 1937 гг. 7Первое присуждение премии Н. И. Лобачевского. Казань. 1898 г. |
загрузка...
